Electricitatea statica
Legea lui Gauss
1. Definitia fluxului electric
Reprezentarea cimpului electric prin linii de cimp reuseste sa inglobeze proprietatile sale esentiale. Am vazut ca, daca densitatea de linii de cimp este facuta sa reprezinte intensitatea cimpului, atunci numarul de linii de cimp are proprietati foarte interesante: se conserva acolo nu exista sarcini si este legat direct de marimile sarcinilor unde isi au capetele aceste linii. De aceea, fizicienii au introdus o marime fizica, numita flux electric, care sa corespunda numarului de linii. Avantajul acesteia este ca poate sa fie exprimata riguros prin vectorul cimp electric.
| Pentru a defini fluxul electric, incepem cu cea mai simpla situatie posibila: o suprafata plana, traversata de un cimp electric uniform, perpendicular pe suprafata. Ca sa calculam numarul de linii de cimp ce traverseaza suprafata nu avem decit sa inversam formula prin care am definit densitatea de linii: numarul de linii este produsul dintre aria suprafetei si densitatea de linii. Cum aceasta din urma corespunde intensitatii cimpului, definim, prin analogie, fluxul electric, ca produsul dintre arie si intensitatea cimpului. Dar cimpul poate avea doua sensuri; ca sa distingem intre ele trebuie sa orientam suprafata, alegind un sens pentru normala la plan. Fluxul este pozitiv cind sensurile cimpului si al suprafetei coincid, si este negativ cind sensurile sunt opuse. | 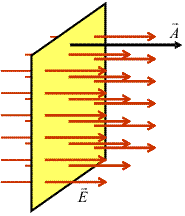 |
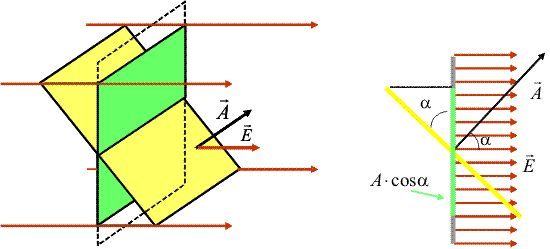
Dar daca suprafata nu este perpendiculara pe cimp, normala sa facind unghiul α cu vectorul cimp electric, ca in figura de mai sus? Se vede din desen ca acum suprafata (desenata cu galben) intercepteaza mai putine linii de cimp, suprafata "efectiva" de interceptie (desenata cu verde) fiind A.cos(α;). Corectam, deci, formula pentru flux, care devine E.A.cos(α;). Aceasta poate fi scrisa intr-o forma foarte compacta daca introducem un vector numit "suprafata orientata", avind modulul egal cu aria si orientarea normalei la suprafata. Astfel, fluxul electric poate fi exprimat ca un produs scalar intre vectorii cimp electric si suprafata orientata
| (Ec. 15.9) |
Lucrurile se complica daca suprafata nu e plana iar cimpul difera de la punct la punct (figura de mai jos). Atunci, trebuie sa impartim suprafata in portiuni mici, atit de mici incit sa fie aproape plane iar pe cuprinsul lor cimpul sa fie aproape unifom.
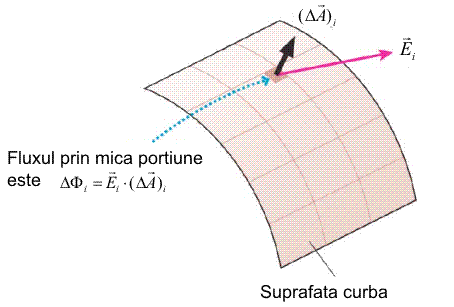
Pentru fiecare portiune a suprafetei, stim sa calculam fluxul ce o strabate, nu trebuie decit sa adunam toate aceste contributii
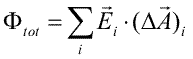 |
(Ec. 15.10) |
Obtinem, astfel, o aproximatie a fluxului total. Cu cit vom face portiunile mai mici, cu atit obtinem un rezultat mai apropiat de valoarea adevarata a fluxului total. Putem, astfel, calcula fluxul electric cu ce precizie dorim.
Exista, pentru suprafetele curbe, doua situatii cu totul particulare, prezentate in figura de mai jos.
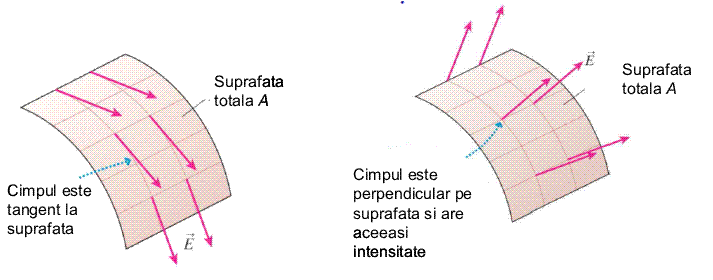
Daca vectorul cimp electric este tangent in orice punct la suprafata respectiva (desenul din stinga), produsul scalar prin care calculam fluxul, este nul. In acest caz, fluxul prin suprafata este zero. Daca, din contra, vectorul cimp electric este, in orice punct, perpendicular pe suprafata (desenul din dreapta), cosinusul din definitie devine egal cu 1. Cind, in plus, intensitatea cimpului in punctele de pe suprafata este constanta, suma precedenta se reduce la produsul dintre acea intensitate si aria totala a suprafetei
| (Ec. 15.11) |
E bine sa retinem aceste situatii simple deoarece le vom utiliza frecvent in continuare.
2. Legea lui Gauss
Suntem acum pregatiti sa culegem roadele efortului depus in definirea fluxului electric. Luam o singura sarcina punctuala (cea mai simpla configuratie de sarcini). Alegem, apoi, o suprafata inchisa, de forma unei sfere de raza r, concentrica cu sarcina. Aceasta suprafata imaginara imparte spatiul in doua regiuni: regiunea interioara si regiunea exterioara. Orientam suprafata sferei spre exterior si calculam fluxul total prin acea suprafata. Stim ca vectorul cimp electric este radial, adica perpendicular, in orice punct, pe suprafata aleasa. In plus, intensitatea sa nu depinde de directie, este aceeasi in orice punct de pe suprafata. Suntem exact in cazul particular discutat mai sus. Pentru a obtine fluxul, trebuie sa inmultim intensitatea cimpului cu aria totala a suprafetei. La distanta r, cimpul produs de sarcina si aria suprafetei sferei au expresiile
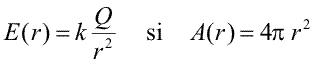 ,
,unde k este constanta lui Coulomb. Astfel, fluxul prin suprafata aleasa este
Observam ca fluxul nu depinde de raza sferei alese ci doar de sarcina electrica din interior, fiind proportional cu aceasta. Acest lucru se intimpla deoarece aria sferei este proportionala cu patratul razei iar intensitatea cimpului este invers proportionala cu patratul razei: modificarea razei nu afecteaza fluxul, care este produsul acestor doua marimi. Daca in interiorul sferei nu ar exista nici o sarcina electrica, fluxul ar fi zero.
Matematicienii pot sa demonstreze riguros ca relatia precedenta ramine valabila pentru orice suprafata inchisa, cum sunt cele din figura alaturata. O asemenea suprafata imaginara inchisa, orientata spre exterior, pe care se calculeaza fluxul electric, este numita suprafata gaussiana. |
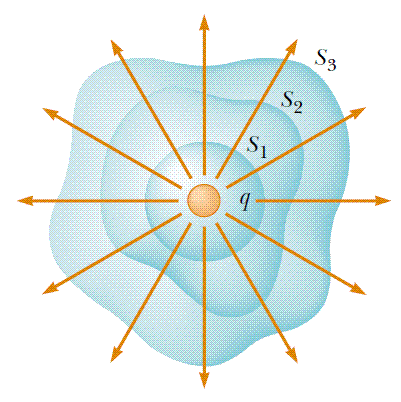 |
Figura de mai jos ne ajuta sa intelegem de ce relatia precedenta este valabila pentru orice suprafata gaussiana. Am desenat, in sectiune, o sarcina punctuala inconjurata de doua astfel de suprafete: una sferica S1 si alta, S2, de forma oarecare.
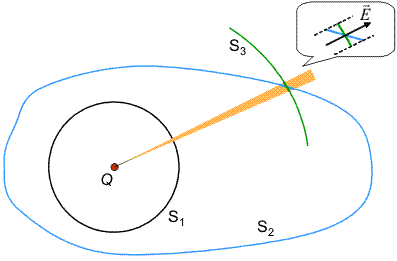
Alegem, in jurul unei linii de cimp arbitrare, un tub subtire de linii de cimp, care are forma unui con si intersecteaza cele doua suprafete (desenat cu portocaliu). Prin punctul de traversare a suprafetei S2 trasam o alta suprafata gaussiana S3 de forma unei sfere concentrice cu sarcina. Conform demonstratiei din paragraful precedent, cele doua sfere intercepteaza fluxuri egale cind sunt traversate de tubul de linii ales. Ar parea ca suprafata S2 intercepteaza un flux mai mare deoarece suprafata sa de interceptie este mai mare decit aceea a suprafetei S3 dar, intersectia nu este perpendiculara. Asa cum se vede in detaliul din dreapta sus, suprafata "efectiva" de interceptie (normala pe vectorul cimp) este aceeasi cu aceea a suprafetei S3. Concluzia acestui rationament este ca si suprafata arbitrara intercepteaza acelasi flux ca cele doua suprafete sferice.
Folosind principiul superpozitiei si adunind fluxul produs de fiecare sarcina in parte, relatia ce exprima fluxul total printr-o suprafata gaussiana poate fi generalizata pentru cazul in care in interiorul suprafatei gaussiene avem un numar arbitrar de sarcini:
| (Ec. 15.12) |
Fluxul prin suprafata inchisa este determinat numai de sarcina neta din interiorul ei, fiind suma fluxurilor produse de fiecare sarcina in parte. Sarcinile din exterior nu contribuie la fluxul prin acea suprafata (vezi figura de mai jos).
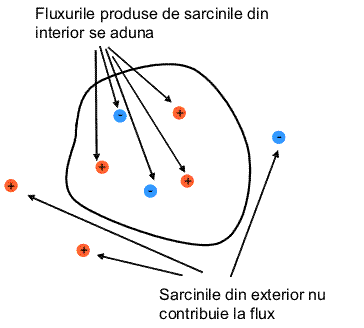
| Rezultatul anterior este numit legea lui Gauss. Legea este respectata si de cimpurile electrice produse de sarcini care nu sunt statice. In figura alaturata, cimpul electric nu este produs de o distributie statica si, de aceea, liniile de cimp sunt curbe inchise care nu pornesc si nu sfirsesc pe sarcini. Fluxul prin suprafata gaussaina este nul asa cum cere legea Gauss. Aceasta, este mai generala decit legea Coulomb, care se aplica doar distributiilor statice de sarcina. | 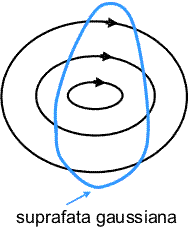 |
Din acest motiv, fizicienii au decis sa simplifice expresia legii lui Gauss, complicind, in schimb, expresia legii lui Coulomb. In loc sa utilizeze constanta lui Coulomb, ei au introdus o alta constanta, numita permitivitatea vidului, prin relatia
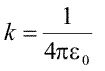 |
(Ec. 15.13) |
esenta trucului constind in factorul 4π. Cu noua constanta, legea lui Gauss se scrie
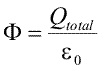 |
(Ec. 15.14) |
iar legea lui Coulomb devine
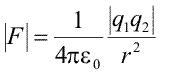 |
(Ec. 15.15) |
Constanta lui Coulomb are valoarea k=8,99.109 N.m2/C2 iar noua constanta, permitivitatea electrica a vidului este ε0=8,85 .10-12 C2/(N.m2). Din considerente de comoditate, unitatea de masura C2/(N.m2) este numita farad/m. Faradul (cu prescurtarea F), va fi introdus intr-o lectie ulterioara.
3. Cimpul electric pentru citeva distributii continue de sarcina
Deseori distantele intre sarcinile dintr-un grup sunt atit mai mici iar numarul lor este atit de mare incit preferam sa consideram ca sarcina este distribuita continuu, fara sa avem spatii fara sarcina. Distributia continua poate sa fie de-a lungul unei linii, pe o suprafata, sau intr-un anumit volum. Chiar daca legea Coulomb se refera la o sarcina punctuala, o putem utiliza pentru aflarea cimpului, daca impartim distributia continua de sarcini in portiuni extrem de fine, cu dimensiuni mult mai mici decit distantele implicate, ca in figura alaturata. Putem sa consideram acele portiuni ca sarcini punctuale, sa calculam cimpul produs de fiecare si, in sfirsit, sa adunam la un loc toate contributiile. |
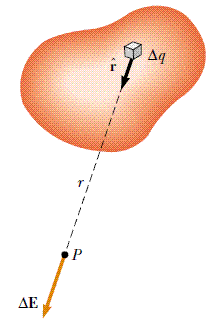 |
Procedura functioneaza intodeauna dar calculele sunt laborioase si trebuie reluate de fiecare data daca modificam distributia de sarcini. In cazul unor distributii cu proprietati de simetrie spatiala, legea lui Gauss permite calculul simplu al cimpului electric, sub forma simbolica (expresie matematica compacta). Sa luam cazul unei sfere de raza R in volumul careia este distribuita omogen sarcina Q. Astfel, densitatea volumica de sarcina (sarcina din unitatea de volum) este
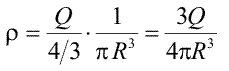
Pentru ca distributia de sarcina are simetrie sferica, vectorii cimpului electric vor fi orientati, obligatoriu, pe directia razei. Alegem o suprafata gaussiana de forma unei sfere cu raza r, concentrica cu distributia de sarcini.
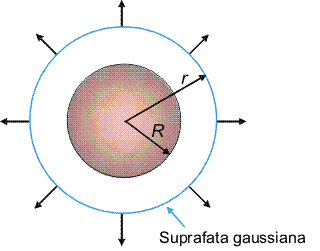
Avem doua situatii distincte. Pentru r>R (figura de mai sus), intreaga sarcina Q se gaseste in interiorul volumului delimitat de acea suprafata si fluxul total, conform legii Gauss, este Q impartit la permitivitatea vidului. Pe de alta parte, in orice punct al suprafetei, cimpul e orientata perpendicular pe suprafata si are aceeasi intensitate. Putem, calcula, astfel, direct fluxul, care este produsul intensitatii cimpului cu aria sferei. Egalam cele doua expresii pentru flux
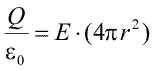
de unde deducem intensitatea cimpului la distanta r
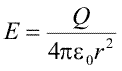
Dar aceasta este expresia cimpului ce ar fi produs daca toata sarcina ar fi concentrata in centru. Orice distributie de sarcina cu simetrie sferica, produce, in exteriorul sau, cimpul pe care l-ar produce o sarcina punctuala, de sarcina egala cu sarcina totala, plasata in centrul distributiei. Pentru aceasta nici nu este necesar ca distributia sa fie omogena, este suficienta doar simetria sferica. Din exterior, o asemenea distributie nu poate fi deosebita de o sarcina punctiforma.

Daca alegem suprafata gaussiana astfel incit r sa fie mai mic decit R (ca in figura anterioara), la flux contribuie, conform legii lui Gauss, numai sarcina din interior. Aceasta poate fi calculata inmultind densitatea de sarcina cu volumul sferei. Egalind cele doua valori ale fluxului (din legea Gauss si din calculul direct),
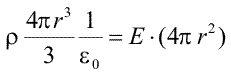
obtinem expresia intensitatii cimpului
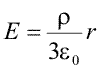 |
(Ec. 15.16) |
In interiorul distributiei, cimpul este proportional cu raza, scazind la zero in centru. Asa cum am vazut, in exterior cimpul merge ca 1/r2. Stringem la un loc cele doua rezultate, desenind graficul cimpului in functie de distanta la centrul distributiei (figura de mai jos).
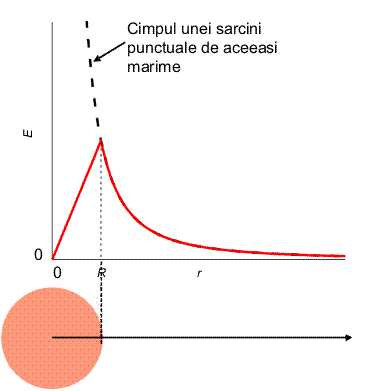
Daca distributia de sarcini este o coroana sferica, in interiorul acesteia cimpul este nul, asa cum se vede in graficul urmator.
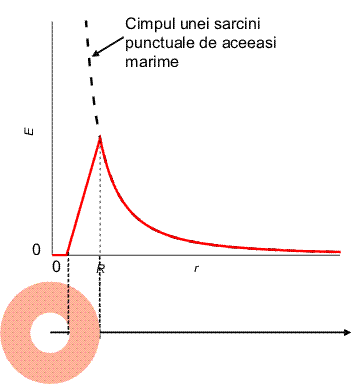
Cind grosimea coroanei sferice devine infinit de subtire, consideram ca intreaga sarcina este distribuita pe o suprafata (distributie superficiala de sarcina). In acest caz, cimpul este nul in interior iar in exterior este acela dat de sarcina punctuala egala cu sarcina totala a distributiei.
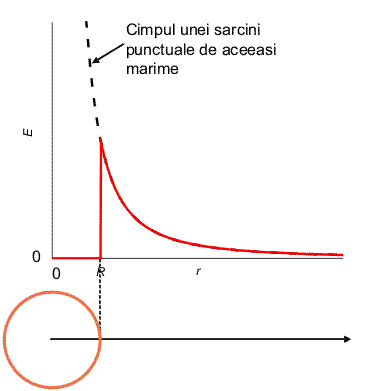
Abordam acum cazul unei distributii liniare de sarcina: de-a lungul unui segment de linie dreapta sarcina este distribuita uniform, cu densitatea liniara (sarcina pe unitatea de lungime) λ. Ne concentram atentia asupra punctului M de la mijlocul "firului" de sarcina si ne intrebam in ce directii pleaca, de acolo, liniile de cimp.
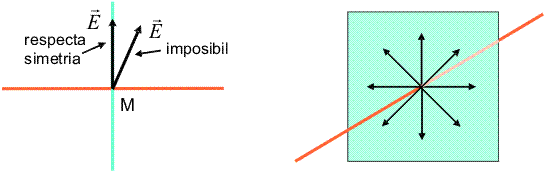
Planul (desenat cu verde in figura de mai sus) ce trece prin M si este perpendicular pe fir (desenat cu rosu) constituie un plan de simetrie pentru distributia de sarcina. De aceea, liniile de cimp in discutie nu au de ce sa mearga nici spre un capat al firului, nici spre celalalt, ele trebuie sa fie continute in acel plan de simetrie (desenul din stinga). In plus, intr-un plan perpendicular pe fir, nici o directie nu are de ce sa fie privilegiata: liniile de cimp au directii radiale, dupa cum se vede in desenul din dreapta al figurii anterioare.
Lansati aplicatia de mai jos si studiati, in 3D, configuratia cimpului creat de un fir incarcat de lungime finita. Cind terminati, nu inchideti aplicatia si nici pagina respectiva. Le veti folosi mai tirziu.
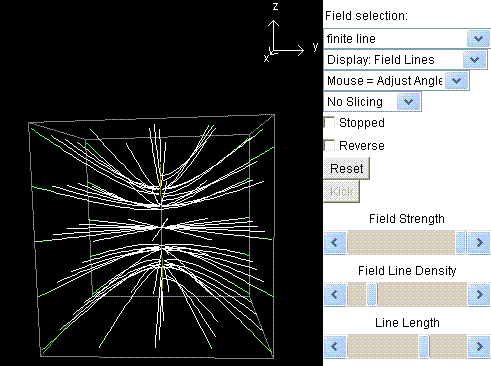
Ati observat ca pentru un punct apropiat de mijlocul firului, liniile devin aproape perpendiculare pe fir daca acesta devine foarte lung. Putem considera, cu aproximatie buna, ca aici este punctul de la mijloc. La limita, cind firul de sarcina devine infinit de lung, orice punct al sau poate fi considerat ca mijlocul sau. Rezulta ca, pentru un fir infinit de lung, toate liniile de cimp sunt drepte, orientate radial, perpendicular pe fir. Verificati acest lucru cu aplicatia pe care ati lasat-o in functiune. Pe pagina respectiva, aveti instructiunile.
Stiind acest lucru, ne este usor sa construim o suprafata inchisa pe care sa putem calcula usor fluxul. Deoarece distributia de sarcina are simetrie cilindrica, alegem un cilindru concentric cu firul, de raza r si lungime l, ca in figura de mai jos.
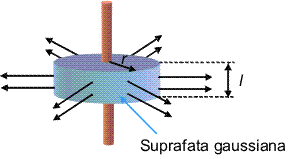
Fluxul prin bazele cilindrului este nul deoarece acolo cimpul electric este tangent la suprafata. Pe de alta parte, pe suprafata laterala a cilindrului, cimpul electric este perpendicular pe suprafata si are aceeasi intensitate in orice punct. Astfel, fluxul prin suprafata inchisa aleasa este E inmultit cu aria suprafetei laterale, care este 2πrl. Sarcina din interiorul volumului delimitat de suprafata aleasa este produsul dintre densitatea liniara de sarcina si lungimea cilindrului, adica λl. Folosind Legea lui Gauss, obtinem un flux λl/ε0. Egalind cele doua expresii gasite pentru flux, obtinem intensitatea cimpului la distanta r fata de fir:
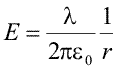 |
(Ec. 15.17) |
Pentru un fir infinit, incarcat uniform, cimpul electric merge invers proportional cu distanta.
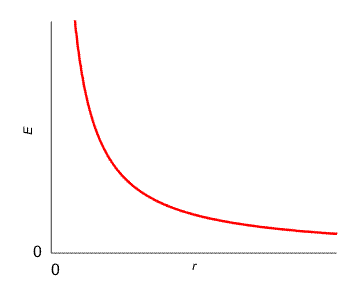
Aceleasi considerente ca mai sus ne ajuta sa calculam cimpul produs de o sarcina distribuita continuu si uniform intr-un cilindru de raza R, infinit de lung, cu densitatea volumica &ro;. In afara cilindrului, cimpul este acela produs de un fir cu densitatea liniara λ=πR2&ro;.
| Daca suprafata gaussiana are raza r mai mica decit R, cum se vede in figura de mai sus, nu toata sarcina de pe distanta l contribuie la flux ci numai cea din interiorul suprafetei. Astfel, | 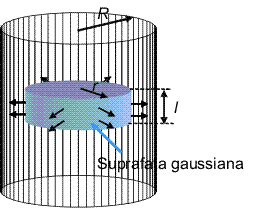 |
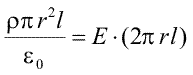
de unde ajungem la
 |
(Ec. 15.18) |
In interiorul cilindrului, intensitatea cimpului este proportionala cu raza, ajungind la zero pe axa.
In sfirsit, ne ocupam de o sarcina distribuita continuu pe suprafata unui disc circular. Distributia este uniforma, cu densitatea superficiala (sarcina pe unitatea de suprafata) egala cu σ. Din considerente de simetrie, in punctul de pe axa discului, cimpul electric este orientat perpendicular pe planul discului, de-a lungul axei. Daca planul incarcat devine infinit, orice punct al sau poate fi considerat centru: liniile de cimp sunt drepte perpendiculare pe plan iar intensitatea cimpului este aceeasi in orice punct de pe plan. Verificati acest lucru folosind aplicatia pe care o aveti inca deschisa.
Pentru aplicarea legii Gauss alegem un cilindru drept, perpendicular pe plan, de raza r si lungime 2l, simetric fata de plan.
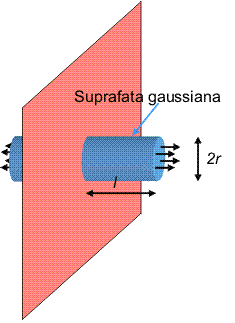
Astfel, fluxul prin suprafata laterala a cilindrului este nul, deoarece cimpul este tangent la aceasta suprafata. Cimpul este perpendicular pe bazele cilindrului si are o intensitate constanta. Astfel, fluxul total este 2Eπr2 (pentru ca avem contributiile egale ale celor doua baze). Pe de alta parte, sarcina din interiorul cilindrului este σπr2. Din egalarea celor doua expresii ale fluxului, rezulta intensitatea cimpului la distanta l fata de plan
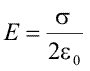 |
(Ec. 15.19) |
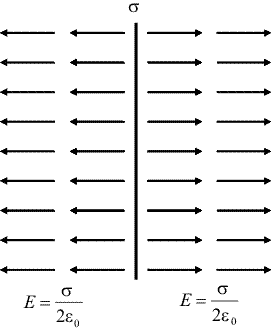
Cimpul electric produs de un plan infinit, uniform incarcat, are aceeasi intensitate la orice distanta fata de plan, asa cum se vede in desenul din dreapta. Planul infinit imparte spatiul in doua; in fiecare jumatate, cimpul este uniform.
Deoarece cimpul este uniform, o sarcina de proba va simti aceeasi forta indiferent de distanta sa pina la plan. Acest rezultat vine in contradictie cu intuitia noastra: inca de la primele experimente de electrostatica am constatat ca fortele cresc cind sarcinile sunt mai apropiate iar legea lui Coulomb formuleaza matematic acest lucru.
Incercam sa intelegem de ce forta rezultanta nu depinde de distanta. Pentru aceasta, delimitam imaginar in planul incarcat uniform o coroana circulara subtire, ca in desenul a) al figurii urmatoare, si ne ocupam de contributia ei la forta asupra sarcinii q. Datorita simetriei, este suficient sa analizam problema intr-o sectiune plana (desenul b). Cind sarcina q este in pozitia A, cele doua portiuni din coroana actioneaza asupra ei cu fortele desenate cu linie neagra. Componentele lor pe axa y se anuleaza reciproc, numai componentele pe axa x (egale intre ele) dau, prin adunare, forta rezultanta, care a fost desenata cu rosu.
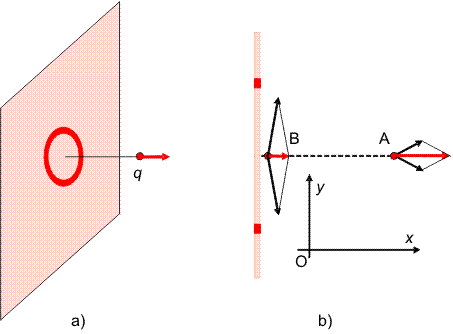
La apropierea sarcinii de plan, in pozitia B, cele doua forte produse de portiunile de coroana cresc in modul, apropiindu-se de o valoare limita, deoarece distanta pina la aceste portiuni nu coboara sub o valoare egala cu raza coroanei circulare. In schimb, componentele lor pe axa x, singurele care contribuie la forta rezultanta, devin din ce in ce mai mici. In concluzie, cind sarcina q se apropie din ce in ce mai mult de plan, forta totala din partea coroanei circulare devine mai mica, apropiindu-se de zero. La o anumita distanta d fata de plan, forta totala asupra sarcinii q este produsa, practic, numai de o portiune din plan de dimensiuni de citeva ori mai mari decit d. Cu alte cuvinte, sarcina q se apropie din ce in ce mai mult de tot mai putina sarcina. Cu cit sarcina q se apropie de plan, distanta d devenind mai mica, desi fortele (conform legii lui Coulomb) cresc ca 1/d2, sarcina care contribuie efectiv la forta rezultanta scade ca d2. Cele doua efecte se compenseaza reciproc si forta rezultanta nu depinde de distanta.
Ne vom intilni in lectiile urmatoare cu situatia in care doua asemenea plane infinite, incarcate uniform cu densitatile de sarcina s si, respectiv, -s, sunt asezate paralel, la o anumita distanta. Dupa cum se vede in figura alaturata, unde sistemul este desenat in sectiune, cimpurile produse de cele doua plane sunt egale si opuse intre ele in afara planelor. Astfel, cimpul in exterior este nul in orice punct (figura de mai jos). |
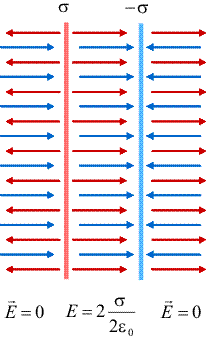 |
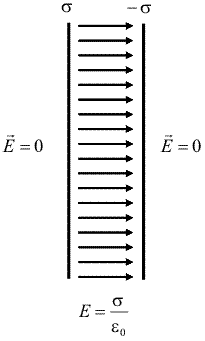
Intre plane, insa, cimpurile produse de cele doua distributii au acelasi sens si intensitatea cimpului total este de doua ori mai mare decit acela produs de un singur plan
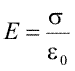 |
(Ec. 15.20) |
 |
Verifica ce ai inteles |

