Electricitatea statica

Calculul potentialului si energiei potentiale pentru o configuratie de sarcini

1. Potentialul produs de un sistem de sarcini punctuale

In lectia precedenta am introdus potentialul electric, am descoperit proprietatile acestuia, si am invatat sa calculam vectorul cimp electric intr-un punct arbitrar din valorile potentialului din vecinatatea acestui punct. Pentru un sistem de sarcini punctuale, avem o formula (Ec. 15.2) ce ne permite sa calculam direct cimpul electric in orice punct M:

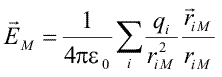(Ec. 16.7)

Totusi, nu am dedus, inca, o expresie similara pentru potentialul creat de aceasta distributie de sarcini

Cautam, mai intii, expresia potentialului creat de o sarcina Q la distanta r. Conform definitiei, acesta este lucrul mecanic efectuat de cimp asupra unei sarcini unitate, pentru a o deplasa din punctul respectiv la infinit. Cum lucrul mecanic nu depinde de drum, alegem sa deplasam sarcina pe directie radiala. Astfel, forta are, in orice punct, directia si sensul deplasarii. In figura de mai jos, am reprezentat forta electrica in functie de pozitie. Pentru o deplasare foarte mica, forta este practic constanta, si "portia" de lucru mecanic efectuat este

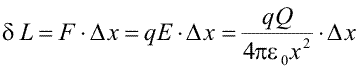
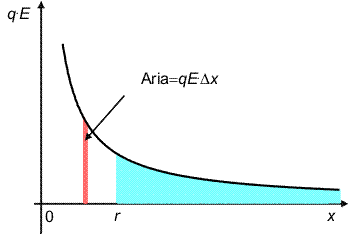
Aceasta este egala cu "aria" suprafetei colorate cu portocaliu. Pentru ca deplasarea e mica, forta ramine aproape constanta si putem sa aproximam forma acestei suprafetei cu un dreptunghi, justificind formula anterioara. Pina la infinit este, insa, drum lung si trebuie sa calculam intregul lucru mecanic, adica toata "aria" albastra de sub graficul fortei, de la raza r la infinit. Aceasta suprafata nu poate fi aproximata in nici un fel cu un dreptunghi. Matematicienii pot sa demonstreze ca aceasta arie este finita si are valoarea


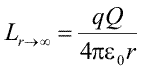
Pentru a afla valoarea potentialului la distanta r de sarcina Q nu mai avem decit sa impartim lucrul mecanic de mai sus la sarcina de test q. Obtinem

(Ec. 16.8)

Expresia potentialului este asemanatoare cu expresia intensitatii cimpului creat de aceasta sarcina. Singura diferenta este ca distanta r de la numitor este, pentru potential, la puterea 1. Potentialul electric creat de o sarcina punctuala merge invers proportional cu distanta pina la sarcina, cimpul electric merge invers proportional cu patratul acestei distante. Folosind principiul superpozitiei si relatia intre cimp si potential, se poate demonstra ca potentialul produs in punctul M de un sistem de sarcini punctuale se obtine din insumarea potentialelor produse in acel punct de fiecare sarcina in parte.

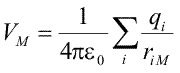(Ec. 16.9)

2. Cimpul si potentialul pentru citeva distributii de sarcina

Avind la dispozitie ecuatii simple pentru potentialul creat de sarcinile punctiforme, sa exploram evolutia spatiala a potentialului si cimpului electric pentru citeva configuratii de sarcini. Vom intelege, astfel, mai bine, legatura intre aceste doua marimi. In figura de mai jos am reprezentat, pentru o sarcina punctuala, potentialul si cimpul electric pe o axa x ce trece prin punctul unde este pozitionata sarcina.

Rata de variatie a potentialului cu pozitia, adica cresterea lui V impartita la cresterea lui x, este panta graficului potentialului. Aceasta panta este pozitiva in stinga originii (unde graficul este crescator) si negativa in dreapta originii, unde graficul este descrescator. Stim din lectia precedenta ca proiectia cimpului pe axa este egala cu aceasta panta, luata cu semn schimbat. Din acest motiv, cimpul electric pe directia axei este negativ in stinga originii (este orientat spre stinga) si pozitiv in dreapta originii.
Daca alegem axa astfel incit sa nu treaca prin punctul unde este sarcina, obtinem potentialul si proiectia pe axa a cimpului din figura urmatoare.


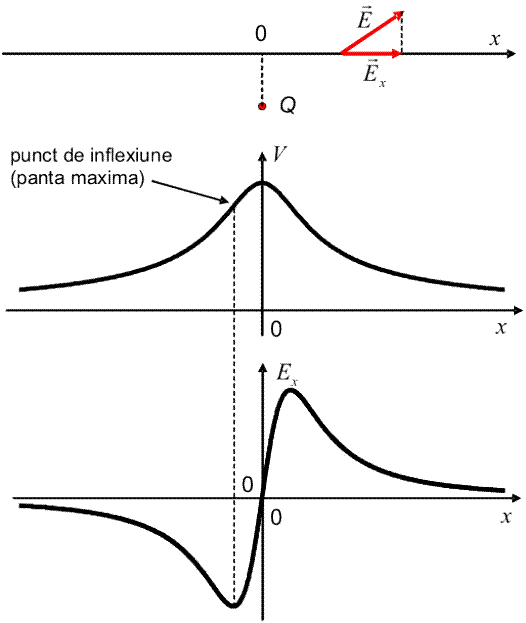
De data aceasta, potentialul are un maxim local, la x=0. Aici panta graficului este zero si, in consecinta, si proiectia cimpului pe axa va fi nula in acest punct. Panta graficului potentialului are valori maxime (in modul) la punctele de inflexiune, acolo unde se schimba curbura graficului (din convexa in concava sau invers). Acestea sunt punctele unde modulul proiectiei cimpului atinge valorile maxime.

Pentru o sarcina distribuita uniform pe suprafata unei sfere de raza R, potentialul si cimpul electric variaza ca in figura de mai jos.


Am aratat, folosind legea lui Gauss, ca in exteriorul sferei cimpul este acela care ar fi produs de o sarcina punctuala cu valoarea egala cu sarcina totala de pe sfera. Cind calculam potentialele punctelor din exterior si de pe sfera, trebuie sa ducem, de acolo, la infinit sarcina de test. Conteaza, deci, numai lucrul mecanic efectuat in aceasta regiune. Astfel, potentialul in afara sferei si pe suprafata ei este exct potentialul ce ar fi creat de sarcina punctiforma. Tot cu legea Gauss am aratat ca in interiorul sferei cimpul este nul. Cum acesta este egal cu panta graficului potentialului (luata cu semn schimbat), rezulta ca in interiorul sferei potentialul trebuie sa aiba panta nula adica sa fie constant, pastrindu-si valoarea atinsa pe suprafata sferei. Oriunde potentialul nu se schimba de la o pozitie la alta, cimpul electric este nul iar, daca intr-o regiune din spatiu cimpul e nul, potentialul e constant in acea regiune.

3. Energia potentiala a unui sistem de sarcini punctuale

Am definit potentialul electric prin energia potentiala a sarcinii de test, deplasata in cimpul electric creat de niste sarcini fixate. Aceasta energie poate fi "recuperata" la ducerea sarcinii de test la distanta infinita. Dar, si dupa ce am indepartat sarcina de test, sistemul de sarcini care produce cimpul mai are energie potentiala, datorita interactiei reciproce intre sarcini. Aceasta energie potentiala este egala cu lucrul mecanic efectuat de cimp pentru indepartarea la distante infinite intre ele a tuturor sarcinilor din sistem. Alternativ, energia potentiala a unei configuratii de sarcini este lucrul mecanic pe care trebuie sa-l efectuam din exterior pentru a aduce toate sarcinile din sistem de la infinit in pozitiile lor actuale. Calculam, mai intii, energia potentiala a unui sistem de doua sarcini punctuale, separate prin distanta r₁₂. La ducerea de la infinit a primei sarcini, q₁, lucrul mecanic e nul deoarece nu exista (inca!) alta sarcina care sa exercite o forta electrica asupra ei. In continuare, fixam sarcina proaspat adusa si incercam sa aducem de la infinit sarcina q₂. De data aceasta, trebuie sa efectuam un lucru mecanic, deoarece sarcina simte o forta electrica din partea sarcinii q₁. Suntem, de fapt, exact in conditiile in care am calculat potentialul unei sarcini punctuale, sarcina de test numindu-se acum q₂. Putem astfel, folosi rezultatul de acolo. Energia potentiala a unui sistem de doua sarcini punctuale este

(Ec. 16.10)

Incercam, acum, sa gasim o expresie pentru energia unui sistem cu numar oarecare de sarcini punctuale. Pentru inceput, abordam un sistem format din trei sarcini. Primul pas a fost deja facut, avem un sistem de doua sarcini si stim cit lucru mecanic am cheltuit ca sa il asamblam. Acum efixam cele doua sarcini q₁ si q₂ in pozitiile lor si aducem, de la infinit, o sarcina q₃. Conform principiului superpozitiei, forta totala asupra acestei sarcini este suma fortelor individuale produse de q₁ si q₂, fiecare din ele calculate cu legea lui Coulomb, ca si cum sarcinile ar actiona separat. Cind sarcina q₃ efectueaza o mica deplasare, lucrul mecanic trebuie calculat prin produsul scalar dintre forta si deplasare. Dar forta este o suma de doi termeni, corespunzatori sarcinilor q₁ si, respectiv, q₂. Rezulta ca lucrul mecanic necesar aducerii sarcinii q₃ este suma a doua lucruri mecanice: cel necesar daca ar fi numai sub actiunea sarcinii q₁ si cel necesar daca ar fi numai sub actiunea sarcinii q₂. Fiecare dintre acestea poate fi exprimat simplu, folosind formule similare cu cea anterioara, asa ca lucrul efectuat de forta externa este

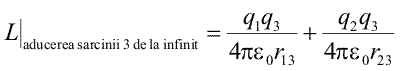
Am construit sistemul de trei sarcini, pe rind, aducind-o pe fiecare de la infinit. In primii doi pasi am realizat un sistem cu sarcinile 1 si 2, a carui energie potentiala W₁₂am scris-o mai sus. Pentru a afla energia potentiala a intregului sistem cu mai trebuie sa adunam lucrul mecanic necesar aducerii sarcinii 3. Obtinem, astfel,

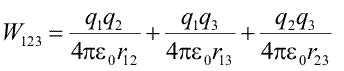(Ec. 16.11)

Ordinea in care aducem sarcinile nu are nici o importanta, expresia energiei potentiale ramine aceeasi. Acest lucru se poate verifica privind cu atentie forma expresiei: puteti permuta intre ei, dupa dorinta, indicii 1, 2 si 3, si expresia ramine nemodificata. Fiecare dintre cei trei termeni se refera la o pereche de sarcini ale sistemului, reprezentind energia potentiala a unui sistem alcatuit numai din aceasta pereche de sarcini.

Ultima observatie ne permite sa generalizam expresia energiei potentiale pentru un sistem alcatuit dintr-un numar oarecare N de sarcini punctiforme, q₁, q₂, q₃, ... , q_N. Mai intii identificam toate perechile (q_i-q_j) care se pot forma. Avem grija sa nu luam o pereche de doua ori, de exemplu perechea (23) este acelasi lucru cu perechea (32). Apoi adunam energiile potentiale ale tuturor perechilor

(Ec. 16.12)

Putem face un truc pentru a scapa de grija alcatuirii perechilor. Cum inmultirea scalarilor este comutativa iar distanta r_ij este tot una cu distanta r_ji, despartim expresia energiei unei perechi astfel:
Cu aceasta, putem scrie energia totala ca

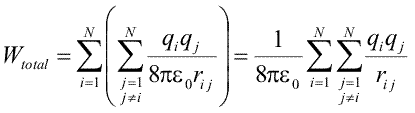(Ec. 16.13)

Indicii celor doua sume merg de la 1 la N, evitind combinatiile in care ei au valori egale.

Am obtinut expresia energiei potentiale pentru o configuratie oarecare de sarcini electrice, exprimata in doua formule echivalente. Cu toate acestea, nu suntem multumiti pe deplin: am introdus potentialul electric legat de o anumita energie potentiala, dar tocmai potentialul nu apare in expresia energiei potentiale a sistemului de sarcini. Suntem, insa, mult mai aproape decit va imaginati de o formulare care sa contina potentiale. Nu avem decit sa aranjam ultima ecuatie, profitind de faptul ca o constanta poate fi scoasa ca factor in afara sumei

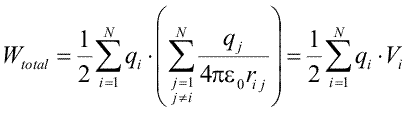(Ec. 16.14)

Expresia din paranteza, pe care am notat-o cu V_i, este potentialul creat, in punctul unde se gaseste sarcina i, de catre toate sarcinile sistemului (mai putin sarcina i). Cu alte cuvinte, pentru fiecare sarcina din sistem, trebuie sa calculam potentialul in punctul in care se afla ea, ignorind propria sa contributie, si sa inmultim acest potential cu valoarea sarcinii. Produsul reprezinta lucrul mecanic ce ar trebui facut pentru aducerea acestei sarcini de la infinit, daca toate celelalte sarcini ar fi fixate in pozitiile lor actuale. Apoi, trebuie sa adunam contributiile de la fiecare sarcina si, in final, sa impartim la doi. Rezultatul este energia potentiala totala a sistemului de sarcini.

Rezultatul anterior este foarte important. El permite calculul energiei unei distributii continue de sarcina. Sa luam, de exemplu, o sarcina totala Q distribuita uniform, cu densitatea superficiala σ, pe suprafata unei sfere de raza R. Alegem un punct arbitrar pe sfera si delimitam o suprafata mica ΔS, pe care se gaseste sarcina ΔQ=σΔS.

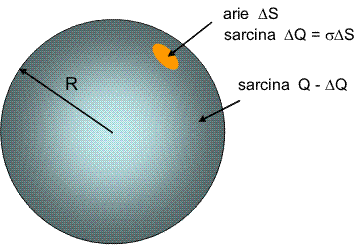
Cit este potentialul in acest punct creat de sarcina de pe sfera cu exceptia lui ΔQ? Daca nu ar fi trebuit sa dam la o parte contributia lui ΔQ, potentialul ar fi fost Q/(4πε₀R). Daca facem insa suprafata ΔS din ce in ce mai mica, si sarcina ΔQ va deveni mai mica, apropiind-se de zero oricit dorim, deoarece am presupus o distributie continua, fara sarcini punctuale. Putem astfel, in aceste conditii, sa spunem ca potentialul creat de restul sarcinii este oricit de apropiat dorim de valoarea Q/(4πε₀R). Contributia la suma energiei potentiale data de sarcina ΔQ este deci ΔQ^.Q/(4πε₀R). Adunind toate contributiile de la diferitele portiuni, si impartind la doi in final, ajungem la expresia energiei potentiale totale

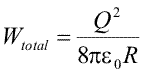(Ec. 16.15)