Electricitatea statica
Capacitatea electrica. Condensatoare
Am vazut ca, daca stim pozitiile si marimilor tuturor sarcinilor (distributia de sarcina electrica) si dorim sa aflam cimpul electric in orice punct din spatiu, metoda este extrem de simpla. Calculam contributia la cimpul electric a fiecarei sarcini punctuale Qj (sau a fiecarei portiuni mici Qj din distributia continua), utilizind formula

si apoi adunam toate aceste contributii. Vectorul rjM merge de la pozitia sarcinii j pina in punctul M unde calculam cimpul. Pentru un calculator modern, calculul si insumarea contributiilor dureaza mult mai putin decit introducerea informatiilor despre distributia de sarcini. Lucrurile se simplifica si mai mult daca, in locul vectorului cimp electric, calculam, mai intii, potentialul, care este o marime scalara. Din variatia spatiala a acestuia, putem sa determinam, apoi, cimpul electric.
Folosind ceea ce am invatat despre cimpul electric, putem sa rezolvam, insa, o problema cu totul diferita. Sa presupunem ca avem un singur corp, de forma oarecare, ce este conductor. Pe el exista o cantitate de sarcina neta Q pe care o stim. Putem calcula cimpul electric produs de acest corp, la echilibru electrostatic? Deosebirea de cazul precedent este ca acum nu cunoastem de la inceput distributia de sarcina, stim doar sarcina totala. Va trebui sa aflam si cimpul electric si distributia de sarcina, ambele dupa atingerea echilibrului electrostatic. Stim, din lectia precedenta ca, la echilibru electrostatic, sarcina in exces se va gasi doar pe suprafata conductorului si ca se va aranja acolo astfel incit cimpul electric in interiorul corpului sa fie nul. Mai stim despre cimpul electric ca are doua proprietati fundamentale: lucrul mecanic nu depinde de drum si fluxul electric printr-o suprafata inchisa este sarcina continuta in acea suprafata impartita la permitivitatea vidului (legea Gauss). Matematicienii pot sa demonstreze ca, pentru corpul conductor respectiv, exista doar o singura distributie de sarcina cu sarcina totala Q care sa genereze un cimp ce indeplineste toate aceste conditii. Cu alte cuvinte, solutia problemei (distrbutia de sarcina si cimpul creat de ea) este unica.
Pentru situatii particulare, cum ar fi cazul unui corp sferic, putem exploata informatii suplimentare, ca simetria. Astfel, distributia de sarcina trebuie sa aiba simetrie sferica, adica sa fie uniforma. Impartind sarcina totala la suprafata sferei obtinem densitatea superficiala de sarcina. Daca impartim si la permitivitatea vidului, obtinem cimpul electric imediat linga suprafata sferei. Acesta este exact cel care ar fi creat de sarcina Q daca ar fi punctuala si plasata in centrul sferei. Simetria sferica a cimpului se pastreaza la orice distanta si, din legea Gauss rezulta ca acesta este egal cu cel al sarcinii punctiforme oriunde in afara sferei. In concluzie, potentialul unui conductor sferic de raza R, incarcat cu sarcina Q, este cel produs de sarcina punctuala la distanta R, adica
 |
(Ec. 18.1) |
Observam ca potentialul conductorului sferic este proportional cu sarcina lui. Trebuie sa accentuam ca ecuatia este valabila numai daca acest conductor este singurul corp din lume. Relatia este verificata cu aproximatie foarte buna daca celelate corpuri sunt la distanta extrem de mare.
Cind corpul are o forma oarecare, nu mai exista metode miraculoase prin care sa calculam "formula" de distributie a sarcinii. Putem, insa, fara sa o calculam, sa facem o afirmatie foarte puternica. Sa presupunem ca, pentru sarcina totala Q, am gasit cumva acea distributie pe suprafata, distributie care produce cimp nul in interiorul corpului.
Ce se intimpla cu cimpul daca densitatea de sarcina se mareste, in orice punct de pe suprafata sa, de a ori ? In primul rind, sarcina totala devine de a ori mai mare (figura de mai jos).
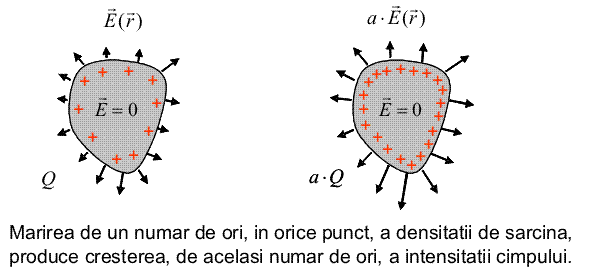
Apoi, nu este greu de vazut ca, in orice punct din spatiu, cimpul electric isi va pastra directia si sensul dar va deveni de a ori mai intens, deoarece contributia fiecarei mici portiuni ce contine sarcina va fi de a ori mai mare. Cind inmultim zero cu a, obtinem tot zero: noua distributie produce in interiorul corpului un cimp ce este, in continuare, nul. Noul cimp (care este cel vechi multiplicat cu a) este solutia pentru noua problema, in care corpul este incarcat cu sarcina aQ. Lucrul mecanic pentru aducerea pe sfera a sarcinii de test (de la infinit) a devenit si el de a ori mai mare, deci potentialul a crescut de a ori. Ajungem, astfel la urmatoarea concluzie:
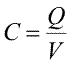 |
(Ec. 18.2) |
Deoarece conditia ca celelalte corpuri sa fie extrem de indepartate (la infinit) este esentiala, se spune ca aceasta capacitate este definita in raport cu infinitul. Capacitatea se masoara in coulombi pe volt. Aceasta unitate poarta un nume special, farad. 1F=1Q/1V. Folosind expresia potentialului conductorului sferic, dedusa mai sus, se obtine capacitatea sa
| (Ec. 18.2) |
O sfera metalica cu diametrul de 10 centimetri are o capacitate de 5,5.10-12 F, adica 5,5 picofarazi. Aceasta se intimpla indiferent daca sfera este masiva sau goala in interior, pentru ca, asa cum stim, sarcina neta se repartizeaza doar pe suprafata.
Cum putem, totusi, calcula, pentru un conductor cu o forma oarecare, distributia de sarcina? Intr-un singur fel, prin incercare si eroare. Presupunem o distributie oarecare de sarcina si calculam cimpul in interiorul corpului. Daca aceste este nul in orice punct, am gasit solutia (despre care stim ca este unica). Daca nu, modificam distributia si incercam din nou. Ceva similar se intimpla in realitate, inainte sa se ajunga la echilibrul electrostati: electronii se imping incoace si incolo, modificind distributia de sarcina pe suprafata, pina cind cimpul in interior ajunge la zero.
Conceptul de capacitate ne ajuta sa intelegem transferul si repartizarea sarcinilor intre corpuri conductoare aduse in contact. Sa presupunem ca in urma separarii sarcinilor prin frecare, o sfera metalica A cu capacitatea de CA=15 pF a primit o sarcina Q0=100 nC. Aceasta inseamna ca, daca sfera este destul de departata de alte corpuri, potentialul sau va fi V=Q/C=6,7 kilovolti. Departe de ea, avem un corp conductor B, mai mic, cu o capacitate CA de 5 pF, care este neutru (desenul a al figurii urmatoare).
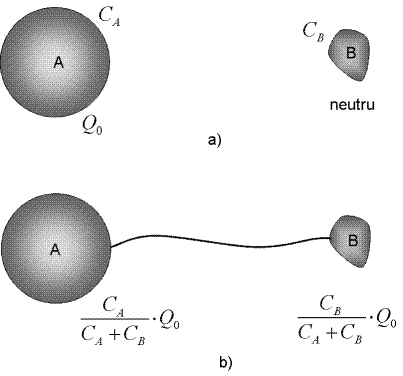
Vrem sa transferam sarcina de pe corpul A pe corpul B, ca in desenul b), legind intre corpuri un fir metalic foarte subtire, astfel incit sarcina de pe fir sa nu contribuie semnificativ la bilant. Primul lucru pe care il putem afirma este ca, dupa legarea firului, cele trei corpuri formeaza un singur conductor, deci ajung la un potential comun, Vf. Indepartam firul (care ia cu el cu foarte putina sarcina) si ne intrebam cita sarcina avem pe fiecare din corpurile A si B. Evident, aceasta este legata de capacitatea corpului respectiv si de potentialul sau: QA=CAVf si QB=CBVf. Concluzia este ca impartirea sarcinii s-a facut proportional cu capacitatile corpurilor: corpul cu capacitate mai mare ramine cu sarcina mai multa. Deoarece sarcina electrica se conserva, iar sarcina de pe fir este neglijabila, corpul B primeste doar un sfert din sarcina disponibila initial pe corpul A, adica numai 25 nC. Daca sfera A este din nou incarcata la 6,7 kilovolti si procesul de transfer se repeta, acum corpul B va ramine cu un sfert din 125 nC, adica 31,2 nC. Aceasta inseamna ca la al doilea transfer sarcina corpului B a crescut cu numai 6,2 nC. Se poate demonstra ca repetind procesul iar si iar, sarcina corpului B va creste lent spre o valoare limita ce este egala cu Q0CB/CA, adica o treime din Q0. Daca cele doua corpuri ar avea capacitati egale, sarcina "finala" a corpului B ar ajunge la Q0 iar, pentru a putea stoca o sarcina mult mai mare decit Q0, este necesar ca sa avem o capacitate a corpului B, pe care stocam sarcina, mult mai mare decit aceea a corpului A.
Am fi asteptat, poate, in experimentul precedent ca, dupa fiecare proces de incarcare-transfer, sarcina de pe corpul B sa creasca cu aceeasi cantitate, astfel incit cu timpul sa acumulam acolo o sarcina considerabila, asa cum acumulam intr-un bazin apa transportata cu o galeata. Legile electrostaticii, insa, ne spun ca nu se intimpla asa. Cu aceasta dificultate se confruntau fizicienii secolului al XVIII-a, care inventasera masini electrostatice pentru separarea sarcinilor, cum este cea din figura din dreapta, sus. Un cilindru de sticla era rotit si incarcat electric prin frecare, sarcina fiind acumulata pe o sfera metalica. Potentialul acesteia ajungea repede la o valoare limita si masina nu mai putea incarca sfera suplimentar. Din intimplare, un experimentator din orasul Leyda (Olanda) descopera prin 1745 ca un container dintr-un material izolator, acoperit pe interior si exterior cu doua foi metalice, poate stoca mult mai multa sarcina decit un conductor de aceeasi marime. Dispozitivul (prezentat in dreapta, figura de jos, impreuna cu "furca" pentru descarcare) a primit numele de "butelie de Leyda" si a dat un nou impuls experimentelor de electrostatica. |
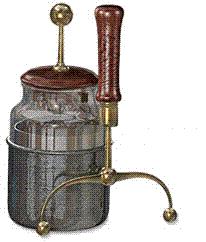 |
Functionarea buteliei de Leyda se bazeaza pe incarcarea celor doua foite conductoare, numite "armaturi", cu sarcini de semne opuse: una din armaturi este incarcata de la un alt corp electrizat iar cealalta, fiind legata la pamint, se incarca prin inductie cu sarcina de semn opus. Fiind foarte apropiate intre ele si atragind-se reciproc, sarcinile de pe cele doua armaturi pot "accepta" alte sarcini transferate din exterior cu mai multa usurinta decit in cazul unui sarcini depuse pe un singur corp. Un astfel de sistem, format din doua conductoare metalice foarte apropiate intre ele, dar care nu sunt in contact, este numit condensator. Butelia de Leyda a fost primul condensator inventat si utilizat de fizicieni. Asa cum vom arata mai jos, condensatoarele sunt utilizate azi la ecranele cu comanda prin atingere, microfoane, aparatele de resuscitare cu socuri electrice si multe alte aplicatii.
De aceea, este important sa studiem un sistem format din mai multe corpuri conductoare, avind sarcinile Q1, Q2, si asa mai departe. Putem lega in vre-un fel potentialele corpurilor de sarcinile de pe ele? Matematicienii numesc combinatie liniara a variabilelor x1, x2, ..., xn o functie de mai multe variabile de forma
Observati ca fiecare termen contine o singura variabila si aceea este la puterea intii. Asa se intimpla la functia ce are graficul o linie dreapta, de unde si denumirea de combinatie liniara. Constantele care inmultesc variabilele sunt numite coeficienti. Vom demonstra, in continuare, ca potentialul fiecaruia dintre corpuri este o combinatie liniara de sarcinile corpurilor, coeficientii fiind constante ce depind doar de geometria sistemului. La prima citire a lectiei, puteti sari peste demonstratie care urmeaza. Merita sa reveniti ulterior asupra ei pentru ca va arata cit de puternic si productiv este principiul superpozitiei
Demonstratie Analizam un sistem format din doua corpuri conductoare, avind sarcinile Q1 si Q2. Consideram, mai intii, sistemul in doua situatii mai simple. Incarcam numai corpul 1 cu sarcina Q1, celelalt avind sarcina zero, ca in desenul a) al figurii urmatoare.
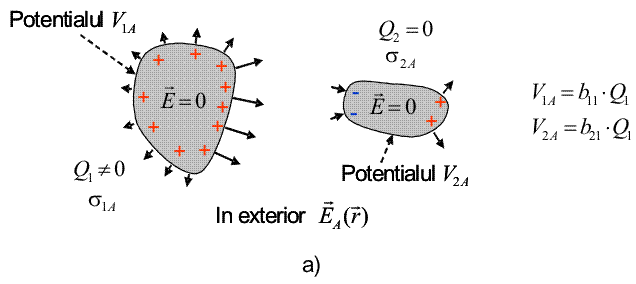
Dupa stabilirea echilibrului, cimpul in interiorul conductoarelor e nul. Desi sarcina totala pe conductorul 2 e nula, densitatea de sarcina de pe suprafata sa nu este nula, pentru ca trebuie compensat, in interior, cimpul produs de corpul 1. Un rationament similar celui din situatia cu un singur corp ne conduce la concluzia ca daca marim de a ori sarcina de pe corpul 1, densitatile superficiale de sarcina se inmultesc cu factorul a, iar vectorul cimp electric devine, in orice punct, de a ori mai mare. In consecinta, si potentialele celor doua corpuri cresc de a ori: ele sunt proportionale cu sarcina Q1. Scriem relatiile de proportionalitate sub forma
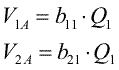
unde coeficienti depind doar de geometria sistemului.
Incarcam acum numai corpul 2 cu sarcina Q2, celalalt avind sarcina neta zero (desenul b) de mai jos).

Un rationament similar cu cel anterior ne conduce la ecuatiile

cei doi coeficienti depinzind numai de geometria sistemului.
Am formulat, in desenele a) si b) doua probleme mai simple. Solutiile lor sunt distributiile de sarcina, cimpurile si potentialele reprezentate pe aceste desene.

Presupunem acum (desenul c) de mai sus) ca, pe fiecare dintre corpuri, densitatea de sarcina este suma densitatilor respective din cazurile a) si b). In acest fel, sarcinile nete de pe corpuri sunt Q1 si Q2, adica cele ale problemei initiale. Principiul superpozitiei spune ca daca am adunat densitatile de sarcina de la cele doua situatii, cimpul electric rezultat va fi, in orice punct, suma cimpurile electrice din fiecare situatie in parte. Rezulta, astfel, pentru situatia c), ca intensitatea cimpului este nula in interiorul conductoarelor. Cum solutia problemei este unica, tocmai am rezolvat problema initiala: stim distributia de sarcina, care este exact suma distributiilor din cazurile a) si b). Daca am adunat cimpurile, trebuie sa adunam si potentialele lor. Obtinem, astfel cele doua potentiale
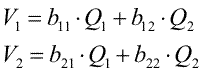 |
(Ec. 18.3) |
Rezultatul anterior poate fi generalizat pentru un numar arbitrar de corpuri conductoare. Pentru un sistem de conductoare la echilibru electrostatic, potentialul fiecaruia dintre ele este o combinatie liniara de sarcinile de pe conductoare. Coeficientii depind numai de geometria sistemului.
Am dedus relatiile intre potentiale si sarcini pentru un sistem oarecare. Sa verificam ca este asa pentru un sistem cu totul particular, la care putem sa calculam usor acesti coeficienti.
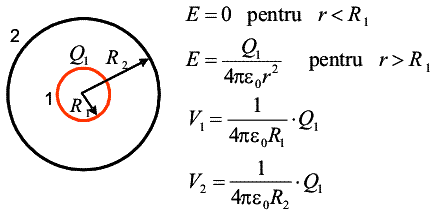
In figura de mai sus este reprezentat un sistem format din doua sfere metalice goale, concentrice. Daca doar sfera interioara este incarcata, cu sarcina Q1, cimpul este, peste tot in afara acestei sfere identic cu cel creat de o sarcina punctuala Q1, asezata in centru. Astfel, pentru potentialele sferelor obtinem expresiile din figura. Incarcam apoi numai sfera exterioara, cu sarcina Q2, ca in desenul urmator.

Cimpul in interiorul ei este nul dar in exterior este acela pe care l-ar produce sarcina punctuala Q2. Cele doua sfere au aceeasi valoare a potentialului. In final, suprapunem cele doua configuratii de sarcina si obtinem potentialele
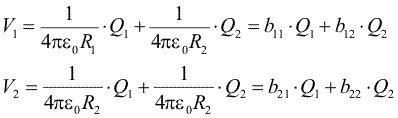
Dupa cum se vede, acestea depind liniar de sarcinile Q1 si Q2. Se observa ca b12=b21. Aceasta nu este o intimplare. Se poate arata ca, pentru un sistem cu numar oarecare de sarcini, bij=bji, oricare ar fi corpurile cu numerele i si j.
In cazul condensatoarelor, cele doua armaturi sunt incarcate cu sarcini egale dar de semne opuse, Q1=Q si Q2=-Q, intre acestea stabilindu-se, astfel, o diferenta de potential U=V1-V2. Folosind relatiile de mai sus, diferenta de potential intre armaturile condensatorului poate fi scrisa ca
Pentru oricare doua conductoare incarcate cu sarcinile Q1=Q si Q2=-Q, diferenta de potential U=V1-V2 este direct proportionala cu sarcina Q. Astfel, putem caracteriza condensatorul prin constanta
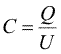 |
(Ec. 18.4) |
care poarta numele de capacitatea condensatorului. Aceasta depinde numai de geometria sistemului (forma armaturilor, distanta dintre ele si orientarea lor relativa). Capacitatea este todeauna pozitiva, adica potentialul armaturii pozitive este mai ridicat decit al celei negative. Am definit mai inainte capacitatea pentru un singur conductor. Putem interpreta aceasta marime ca fiind capacitatea unui condensator, a doua armatura fiind asezata la departare infinita. Din acest motiv, am numit-o capacitate in raport cu infinitul.
Asa cum am spus mai sus, unitatea de masura pentru capacitatea electrica este numita farad, cu prescurtarea F. Valoarea capacitatii unui condensator, in farazi, este sarcina (in modul) a unei armaturi, in coulombi, cind diferenta de potential intre armaturi este de 1 volt.
La descarcarea unei butelii de Leyda se obtine o scinteie impresionanta (mai puternica decit cea care poate fi produsa de masina electrostatica de la care a fost incarcata). Priviti!
Condensatorul inmagazineaza, deci, energie electrostatica. Putem calcula usor cit este aceasta energie daca ne aduce aminte formula pe care am dedus-o pentru energia potentiala a unei distrbutii continue de sarcina. Trebuia sa inmultim fiecare portie de sarcina electrica cu potentialul la care se gaseste, sa adunam contributiile si, in final, sa impartim la doi. Pentru condensator este foarte simplu sa aplicam acest algoritm, sarcina Q se gaseste pe armatura cu potentialul V1 iar sarcina -Q se gaseste pe armatura cu potentialul V2. Adunind cele doua contributii, ajungem la
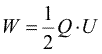 |
(Ec. 18.5) |
Utilizind capacitatea condensatorului, energia unui condensator poate fi exprimata in alte doua forme echivalente:
 |
(Ec. 18.6) |
Pentru un condensator de capacitatea data, energia stocata este proportionala cu patratul sarcinii si, echivalent, cu patratul tensiunii intre armaturi.
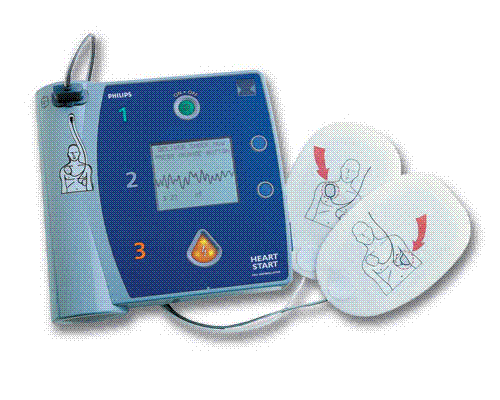
Aplicatie In timpul unui atac cardiac, inima poate intra in fibrilatie ventriculara, batind intr-un un ritm haotic ce pune in pericol viata subiectului. Defibrilatorul (figura alaturata) produce un soc electric controlat, prin intermediul a doua placute de contact numite padele, aplicate pe pieptul subiectului. Astfel, activitatea haotica a inimii este oprita, dind posibilitatea reluarii ritmului ei normal. Socul electric este produs prin descarcarea unui condensator cu o valoare tipica C=100 mF, medicii controlind intensitatea socului prin intermediul energiei stocate in condensator. In mod uzual, aceasta ajunge pe la W=100 J. Utilizind expresiile pentru energia condensatorului, rezulta U2=2W/C, adica U=1400 V, si o sarcina Q=CU=0,14 C. La un defibrilator portabil, energia este furnizata condensatorului de catre o baterie, intr-un interval de ordinul a 10 secunde. Astfel, puterea medie pe care trebuie sa o produca bateria este de (100 J)/(10 s)=10 W. Descarcarea condensatorului prin corpul subiectului dureaza insa mult mai putin, cam 10 ms. Puterea medie furnizata de condensator in timpul defibrilatiei este, deci, (100 J)/(10 ms)=10 kW. |
  |
Condensatoarele pot fi construite cu diferte forme. Sistemul compus din doua sfere concentrice, analizat anterior, este un condensator sferic. Utilizind relatiile intre potentiale si sarcini deduse acolo, ajungem la o valoare a capacitatii
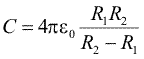 |
(Ec. 18.7) |
| Aceasta capacitate devine cu atit mai mare cu cit scade distanta intre armaturi. Se poate vedea usor ca daca aceasta este o zecime din raza sferei mari, capacitatea condensatorului este de aproximativ 10 ori mai mare decit aceea a unui singur corp sferic de aceeasi raza R2. Trebuie remarcat ca incarcarea armaturilor cu sarcini opuse de modul egal face ca intensitatea cimpului electric sa fie nula in afara sferei mari, adica in exteriorul condensatorului sferic (vezi figura din dreapta). Din acest motiv, pe suprafata externa a armaturii mari nu exista sarcina neta in nici o regiune. Intreaga sarcina -Q de pe armatura mare este distribuita pe suprafata sa interna. |  |
In figura alaturata este prezentat un condensator ale carui armaturi sunt de forma cilindrica. Am aratat intr-o lectie anterioara, folosind legea Gauss, ca o sarcina distribuita uniform pe o suprafata cilindrica de lungime infinita produce in interior un cimp nul. In exterior cimpul este identic cu cel produs de un fir infinit pe care ar fi distribuita uniform sarcina respectiva. Din acest motiv, cind armaturile condensatorului cilindric sunt incarcate cu sarcini opuse si egale in modul, cimpurile produse de cele doua armaturi se anuleaza reciproc in orice punct din exteriorul cilindrului mare. Astfel, in afara condensatorului cimpul este nul iar toata sarcina de pe cilindrul exterior este distribuita doar pe suprafata interioara a acestui cilindru. |
 |

Matematicienii pot sa demonstreze ca diferenta de potential intre armaturi produsa de un asemenea cimp este
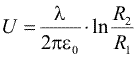
Sarcina unei armaturi, pe o portiune de lungime L, este l.L, astfel ca aceasta portiune din condensatorul cilindric infinit are expresia
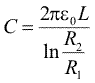 |
(Ec. 18.8) |
unui condensator cilindric infinit de lung)
Pentru un condensator cilindric real, de lungime finita, cimpul in exterior nu este exact zero, abaterile mai importante aparind la capetele cilindrului. Cu toate acestea, daca lungimea condensatorului este mult mai mare decit grosimea sa, capacitatea poate fi calculata cu buna aproximatie utilizind formula de la condensatorul de lungime infinita.
Sa consideram, acum, un condensator alcatuit din doua placi conductoare plane, paralele, separate prin distanta d, ca in desenul a) al figurii urmatoare.

In plus, placile au extindere infinita. Incarcam placile, conform definitiei capacitatii unui condensator, cu densitati de sarcina egale in modul si opuse ca semn, s si -s. Stim ca sarcina se va raspindi numai pe suprafetele placilor. Dar pe care din ele ? Cum regiunea dintre placi nu este o cavitate inchisa, nu suntem in situatia in care densitatea de sarcina sa fie obligatoriu nula pe fetele interioare. Dupa cum spuneam mai sus, solutia unei astfel de probleme poate fi cautata prin incercari. Incepem cu presupunerea ca sarcina este distribuita numai pe suprafetele exterioare, ca in desenul b). Am avea, deci, doua plane infinite, paralele, uniform incarcate, cu densitatile s si -s. In lectia despre legea lui Gauss am aratat ca, pentru un asemenea sistem, cimpul intre plane este uniform si egal cu s/e0. Ar rezulta, deci, un cimp diferit de zero inclusiv in interiorul placilor conductoare (regiunile desenate cu gri). O asemenea distributie nu este o solutie a problemei deoarece nu anuleaza cimpul in interiorul conductoarelor. Incercam, acum, cu sarcina distribuita numai pe fetele interne ale placilor (desenulc). In exteriorul celor doua plane de sarcina cimpul produs va fi nul; este exact de ce avem nevoie, in interiorul conductoarelor cimpul trebuie sa fie zero. Aceasta distributie de sarcini este o solutie a problemei noastre. Si cum solutia este unica, este solutia problemei. Cimpul electric este, deci, nul in afara placilor unui condensator plan infinit iar intre placi cimpul este uniform si are valoarea
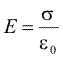 |
(Ec. 18.9) |
unui condensator plan infinit)
Deoarece cimpul este uniform intre placi si este egal cu rata de variatie a potentialului cu pozitia (cu semn schimbat), rezulta ca potentialul placii pozitive este mai ridicat cu valoarea Ed in raport cu cel al placii negative. Pentru o portiune de arie S, sarcina de pe o armatura este sS. Astfel, capacitatea acestei portiuni este
 |
(Ec. 18.10) |
dintr-un condensator plan infinit)
Condensatoarele plane reale au intodeauna extindere finita, asa ca relatia anterioara nu poate fi aplicata strict pentru ele. Cu toate acestea, daca ambele dimensiunii ale placilor sunt mult mai mari decit distanta d dintre armaturi, atunci capacitatea unui condensator plan poate fi calculata, cu buna aproximatie, utilizind relatia de la condensatorul plan infinit. In aceasta situatie, S este chiar suprafata unei armaturi. Nu trebuie sa uitam, insa, ca, pentru un condensator de dimensiuni finite, cimpul in exterior nu este strict zero. De asemenea, desi in centrul placilor cimpul este aproximativ uniform in interior, la marginile placilor acesta este mult diferit, atit ca marime cit si ca directie. Puteti vedea harta liniilor de ecimp si a potentialelor in simularea urmatoare.
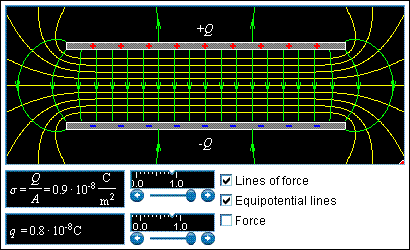
 |
Foloseste experimente virtuale, ca sa intelegi mai bine |

Pentru a deschide o pagina noua, cu experimentul virtual din imaginea de mai sus, apasati pe imagine. Dupa efectuarea experimentului, nu uitati sa inchideti aplicatia si pagina respectva, intorcindu-va aici.
Expresia capacitatii condensatorului plan este importanta pentru ca poate fi aplicata, cu aproximatie buna, si la alte geometrii constructive. Pentru un condensator sferic la care raza mare este doar cu putin mai mare decit raza mica, R2=R1+d, d fiind mult mai mic decit R1, capacitatea poate fi aproximata prin 4pe0R2/d. Dar 4pR2 este chiar suprafata sferei iar d este distanta intre armaturi. Am regasit formula de la condensatorul plan. Si in cazul condensatorului cilindric cu R2=R1+d, d mult mai mic decit R1, aproximarea logaritmului conduce la o formula similara cu aceea a condensatorului plan.
Pentru a economisi spatiu, condensatoarele plane pot fi "rulate", asa cum se poate vedea in figura de mai jos, stinga, unde un asemenea condensator a fost dezmembrat. In dreapta sunt prezentate citeva tipuri de condensatoare produse industrial pentru aparaura electronica.


 |
Verifica ce ai inteles |

